15418 Final Project

Project Summary

The n-body problem is a classical problem of predicting the interactions and movements of particles that all interact with each other. It is an important problem in astrophysics and particle physics. For our final project, we tackled implementing two different n-body simulation algorithms, one using a simple direct method, and the other using a popular tree-based method known as the Barnes-Hut simulation. Parallelization was implemented using the openMP API.

Background

The simulator is for predicting the motion of N individual particles interacting each through gravitation. The motivation behind the project is to simulate N self-gravitating objects, every object interacts with every other object. As a result we need to calculate (N-1) force terms for each particle, leading to total number of N(N-1) calculations to determine the next state of the system. The Newtonian project simulates Particle-Particle (PP) methods.

As an alternative to the parallelized Particle-Particle method, we used Barnes-Hut algorithm to divide the total particle volume into a hierarchical tree which allow for computational costs of O(N log N). This algorithm is more adaptive to high clustering than PP method. The Barnes-Hut algorithm allows grouping distant objects for calculation. The N-body problem has many applications. One of many applications is to model star clusters. The Barnes-Hut project simulates how these star clusters, collections of stars bound tightly by gravity, interact with one another and other clusters.

For both algorithms, we wrote our own visualizations so that we could see the algorithms working in real time, as well as seeing visually how much our parallelization helps improve the performance of the simulation.

Approach

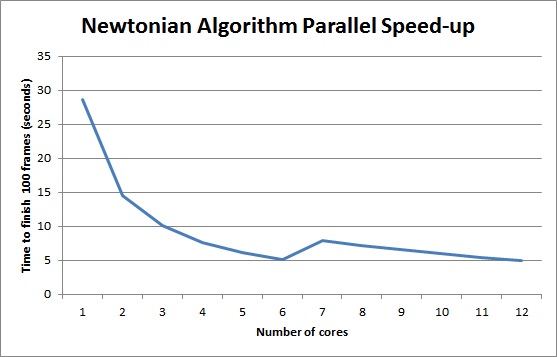
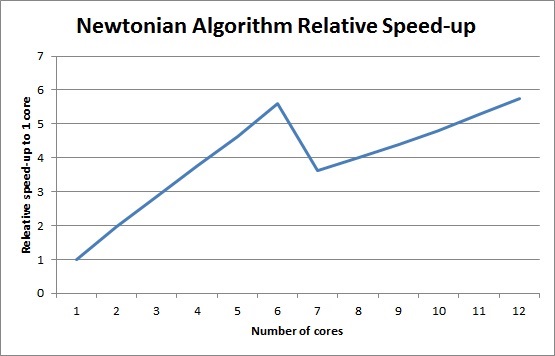
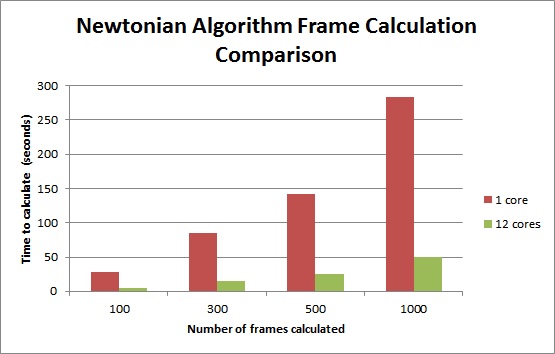
The Newtonian algorithm is fairly easily parallelizeable, so openMP was used to implement parallelization. Each particle was operated on by each iteration of an openMP parallel for loop. However, due to the fact that the algorithm is not a compute-intensive algorithm, the speed-up is bounded by the number of memory operations it does.

For consistency, openMP was also used to implement parallelization for the Barnes-Hut algorithm. The update of each particle by the traversal of the tree was also parallelized, as in the Newtonian algorithm.

Results

Newtonian Algorithm

Visualization of Newtonian Algorithm (dots represent particles)

Barnes-Hut Algorithm

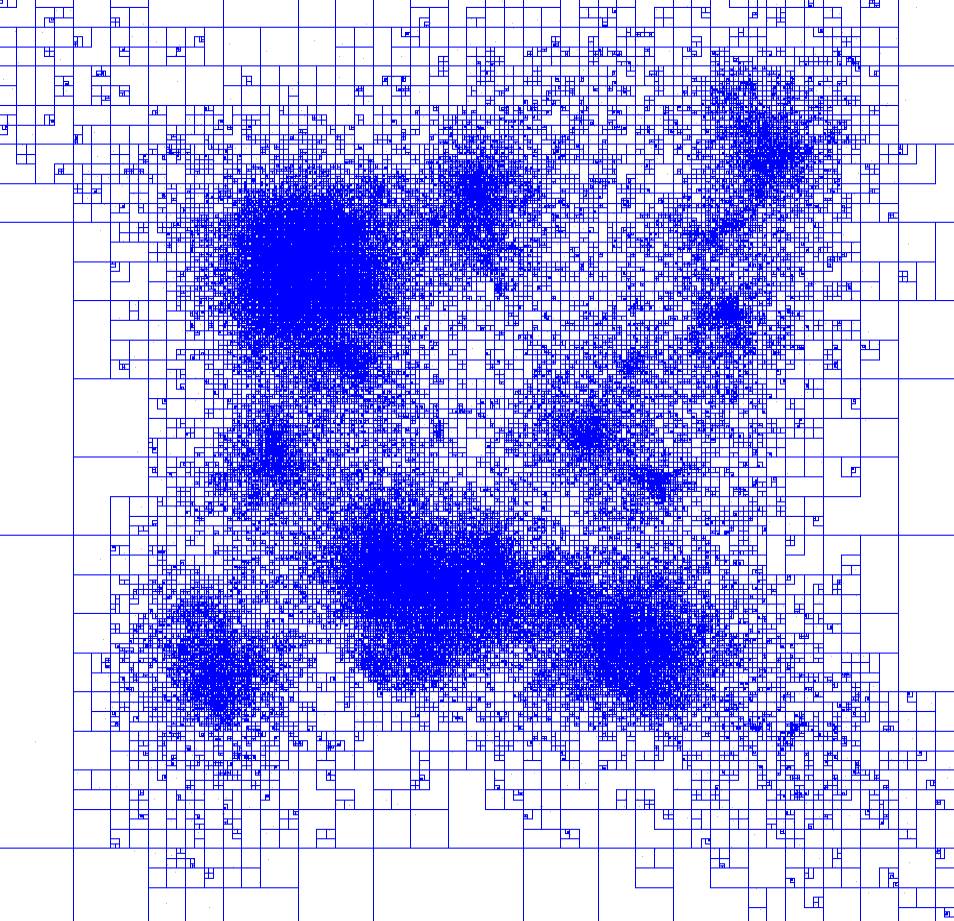
Visualization of Barnes-Hut Algorithm (lines represent quad-tree divisions)

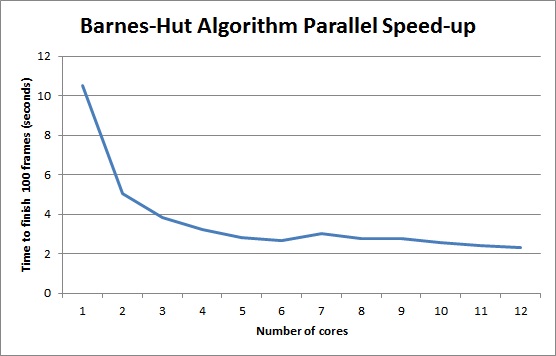
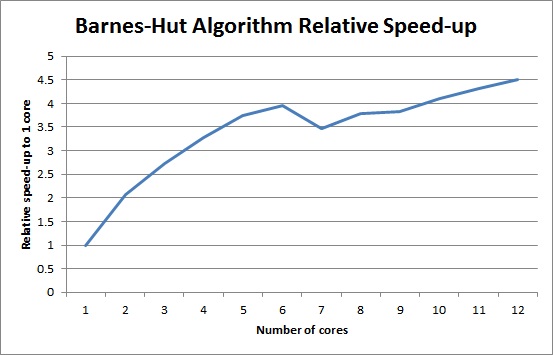
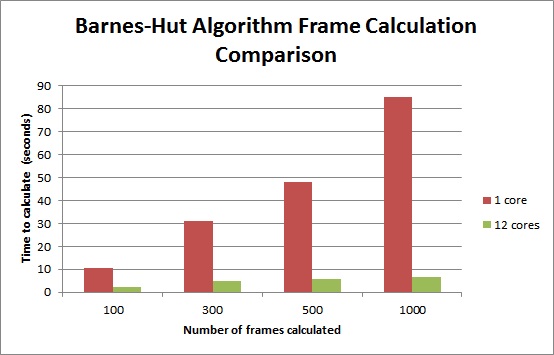
Project Clarifications

We originally were planning on improving the performance of a physics/particle simulation library called Liquidfun. However, after two weeks of going through the code base and trying to understand it, profiling the code, and trying to work with the libraries and code, we decided that the scope of the project was too big and it may not have been possible to meet our goals with the given time constraints. As a result, we decided to switch our project to a comparison of N-Body Simulation Algorithms.

Useful Links

Introduction to N-Body Simulations

Parallel N-Body Simulations Overview

SDL Wikipedia Page

Work Division

Ji Hye: Responsible for implementation of algorithms and visualizations

Bryan: Responsible for parallelization of algorithms, benchmarking, and website